卷积编码
卷积编码和维特比解码具有很强的前向纠错能力,可以全部由软件编程实现,以便节约硬件成本,值得在物联网中推广应用。
物联网(Internet of Things)是连接各种物理节点的一种特殊网络,这些物理节点主要由各种各样的传感器组成,包括温度传感器、湿度传感器、压力传感器和图像传感器等等。随着传感技术和无线通信技术的大幅提升,物联网的各种应用也得到飞速发展,万物互联的时代越来越接近我们的生活。
在物联网蓬勃发展的同时,无线通信不可避免的会产生干扰的问题,这样会导致信号的误码率变高,严重影响系统的稳定性。如果采用CRC、累加和等方式验证数据的正确性,则不能解决数据错误后怎样恢复原始数据的问题。如果采用双向通信验证数据是否正确的方式,则会增加通信时间,导致系统延时加重,影响系统的实时性,而且有的单向通信的场合还不能使用这种方式。
本文专门针对这些问题,提出了一种物联网前向纠错的方案。该方案采用了卷积编码和维特比解码的方式,有效的解决了通信误码率的问题,提高了系统的稳定性和实时性。该方案适用于单向、双向通信模式,在发送端使用卷积编码发送,在接收端使用维特比解码,即使在通信过程中有一定的误码率,系统也能自动纠正错误数据,以达到正确通信的目的。
卷积编码
卷积编码(Convolutional Encoding)由Peter Elias在1955年第一次提出,目前已经广泛应用于信道编码领域。卷积编码可以处理一系列数据位,最大的特点就是输出的数据位不但与输入的数据位有关,而且与输入的数据位前面的数据位有关,即所谓的记忆深度,这样很好的提高了数据容错性能。其编码格式有很多种,本文讲解最基本的(2,1,2)格式,即2-bit输出、1-bit输入和2-bit记忆深度。
请参考图一的卷积编码示意图。图中In, In-1, …, I1, I0为输入数据位;C1, C0为清零位Clear,其初始值为00;F1, F0为补充位Flush,其初始值为00;O1, O0为输出数据位;X1, X2为异或计算器;S为选择开关。每输入一个数据位,便会输出对应的两个数据位。例如当输入I0数据位时,I0对应的输出低位数据位O0的数值为I0, C1, C0的异或值,而I0对应的输出高位数据位O1的数值为I0, C0的异或值。依次计算I1, …, In-1, In对应的输出数据位。为了保证In和In-1这两个数据位的编码完整性,还需要计算F1和F0补充位对应的输出数据位。其中F1对应的输出低位数据位的数值为F1, F0, In的异或值,而F1对应的输出高位数据位的数值为F1, In的异或值。
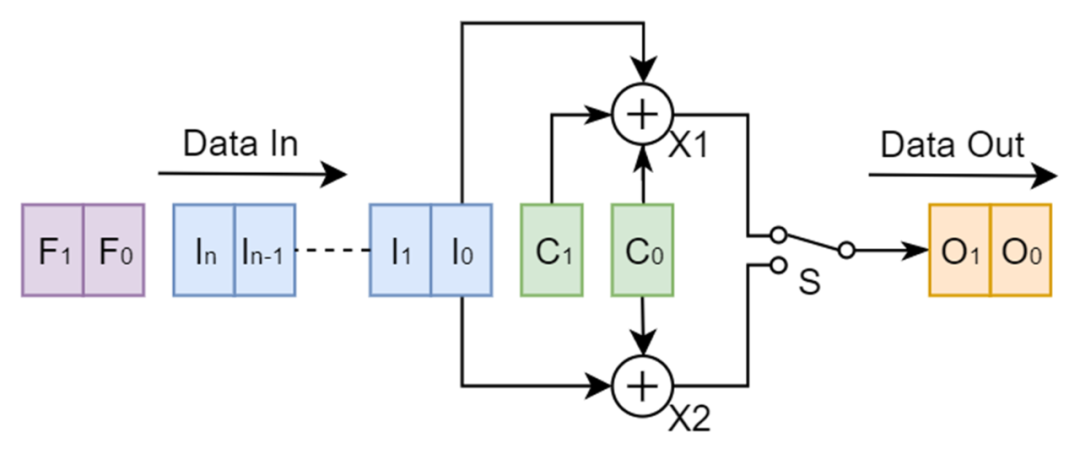
图一
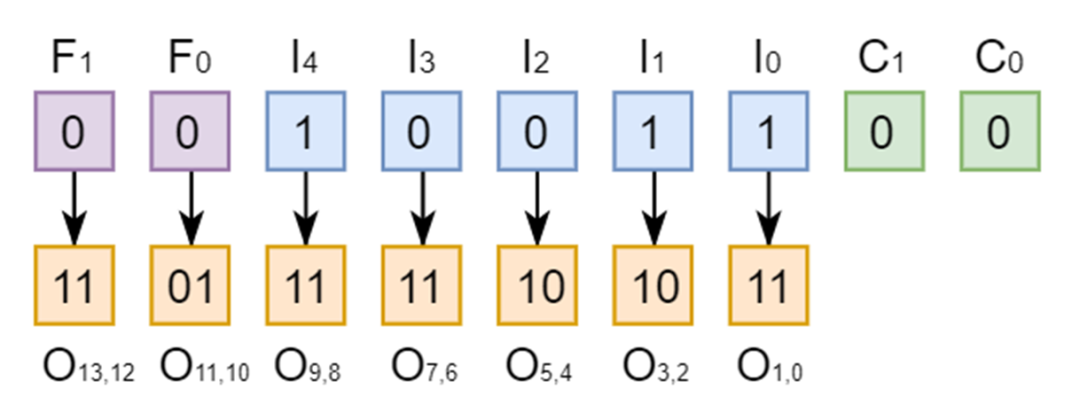 图二
图二
维特比解码
维特比解码(Viterbi Decoding)是由Andrew Viterbi在1967年发明的,并用他的名字命名。维特比解码具有一定的纠错能力,即使接收到的卷积编码数据有一定的误码存在,也可以使用维特比解码恢复出原始数据。
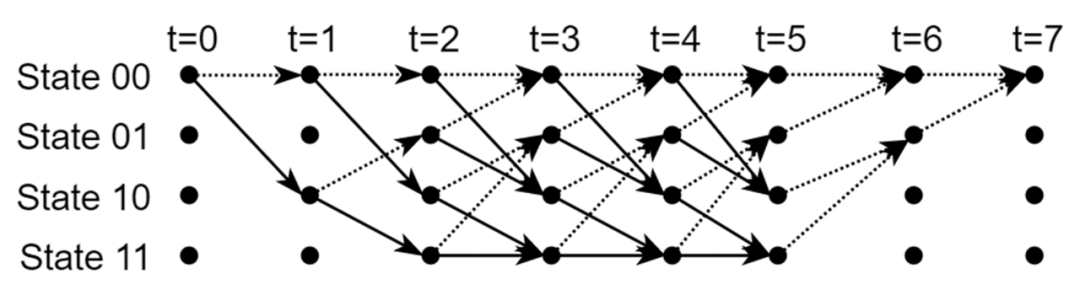
图三
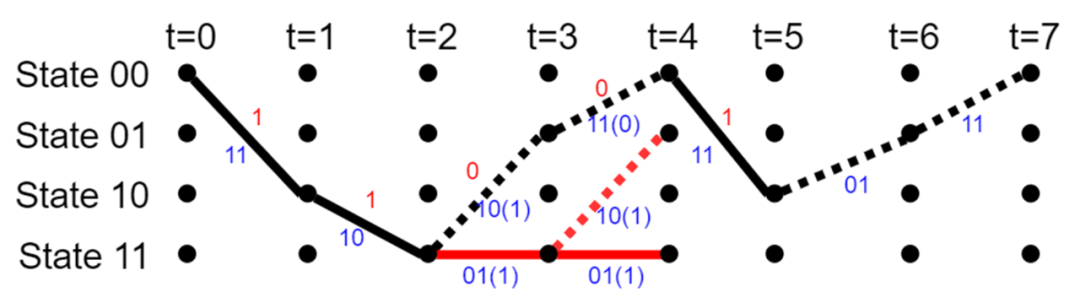
网格图的状态、输入数据和输出数据的关系如图四所示。图中虚线箭头表示输入数据为0时从一个状态转移到另外一个状态,而实线箭头表示输入数据为1时从一个状态转移到另外一个状态。图中左边红色数据表示虚线对应的输出数据,而右边蓝色数据表示实线对应的输出数据。这样输出数据和输入数据就有了一一对应的关系,即得到了输出数据就会推导出对应的输入数据。
 图四
图四
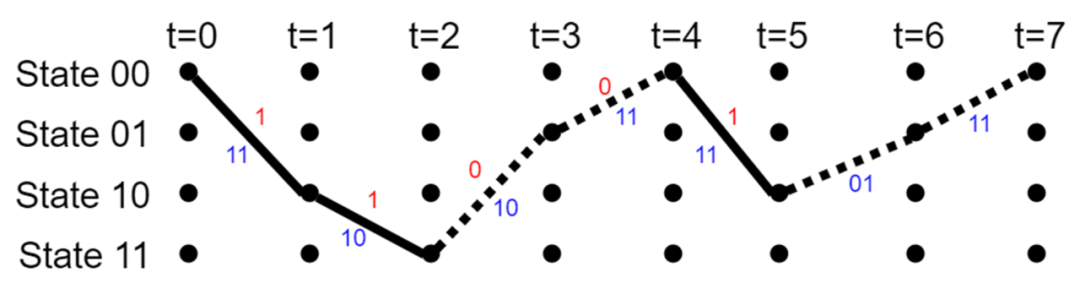
图五
 图六
图六
总结
实践证明,卷积编码和维特比解码具有很强的前向纠错能力,可以全部由软件编程实现,以便节约硬件成本,值得在物联网中推广应用。另外,卷积编码还有不同的编码方式,可以采用私有格式,用以实现通信数据密文发送,起到一定的加密作用,对系统的安全性也有很大的帮助。

 MyArrow™ — 艾睿电子线上系统
MyArrow™ — 艾睿电子线上系统


